4. 로지스틱 회귀

'XX 회귀' 라고 하는 것은, 데이터를 통해 'XX'를 구하는 것이라고 이해할 수 있다. '선형 회귀'에서는 말 그대로 '선'(정확히는 선형방정식)을 찾았다. 로지스틱 회귀에서는 'logistic(기호논리)'을 찾는 것이 목표이다. 그러니까, 어떤 기호값(label)을 분류하는 논리식을 찾는 것이 로지스틱 회귀이다. 논리식이래서 온톨로직한 문장을 찾는건 아니고, 결국에는 선형회귀와 마찬가지로 입력 데이터세트 $X$를 결정 공간에 잘 사상시킬 수 있는 사상 벡터 $W$ 를 찾는게 목표이다.

예를들어 키, 몸무게에 따른 남/여 카테고리 컬럼이 존재하는 경우, 남성과 여성을 구분하는 결정 직선을 구하고자 한다면 로지스틱 회귀를 적용해야 한다.

최소제곱오차에 따른 선형 회귀 방식을 적용하는 경우는 키에 따른 몸무게를 예측하고자 하는 상황과 같이, 이미 존재하는 두 수치 변수간의 관계를 파악하고자 할 때 이다.

위의 사례들에서 알 수 있다시피, 특정 입력 값에 대한 출력값을 예측하는 모델(function)을 구하고자 할 때는 선형회귀를, 레이블이 존재 할 때 입력값들을 구분하고자 하는 기준 function을 구하고자 할 때는 로지스틱 회귀를 적용한다.

그런데 이제, 선형회귀에서는 결정 공간(치역)이 연속적인 값들로 구성되어 있지만, 로지스틱에서는 결정 공간이 레이블 값(흔히 0, 1)로만 구성되어 있다. 그래서 로지스틱 회귀에서는 시그모이드 함수에 사상된 벡터를 넣어서 0~1사이의 값으로 바꿔버린다.

엄밀히 따지면, 로지스틱 회귀에서 $wx+b$, 즉 $W^T\cdot X$ 갖는 의미는 W와 X의 내적을 의미하고, 내적이라는 것은 곧 $W$가 $X$의 성질을 얼마나 잘 반영하고 있는지(닮았는지)를 의미한다. 즉, $W$라는 것은, 어떤 특정한 레이블을 갖는 데이터 집합에 대한 벡터라고 할 수 있다.

따라서 $w^{t}x$가 직교, 즉 0의 값을 가지면 완전히 상이함을, 양/음의 값을 가지면 x 벡터와 w벡터가 어느정도 유사성을 띄고 있음을 의미한다. 여기에 시그모이드 함수를 적용함으로써 계산된 값을 확률적으로 표현하게 된다.

$w$와 $w_0(=b)$의 값에 따라 시그모이드 함수가 조정되며 성능이 향상되는 과정을 간단히 보면 아래 사진과 같다.

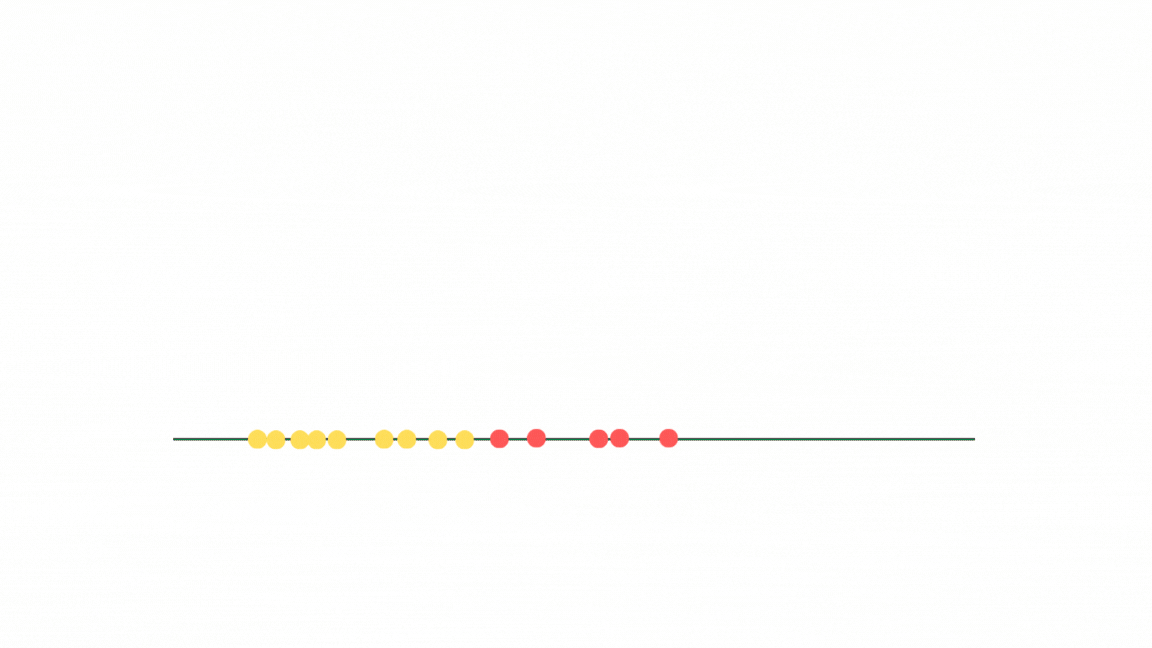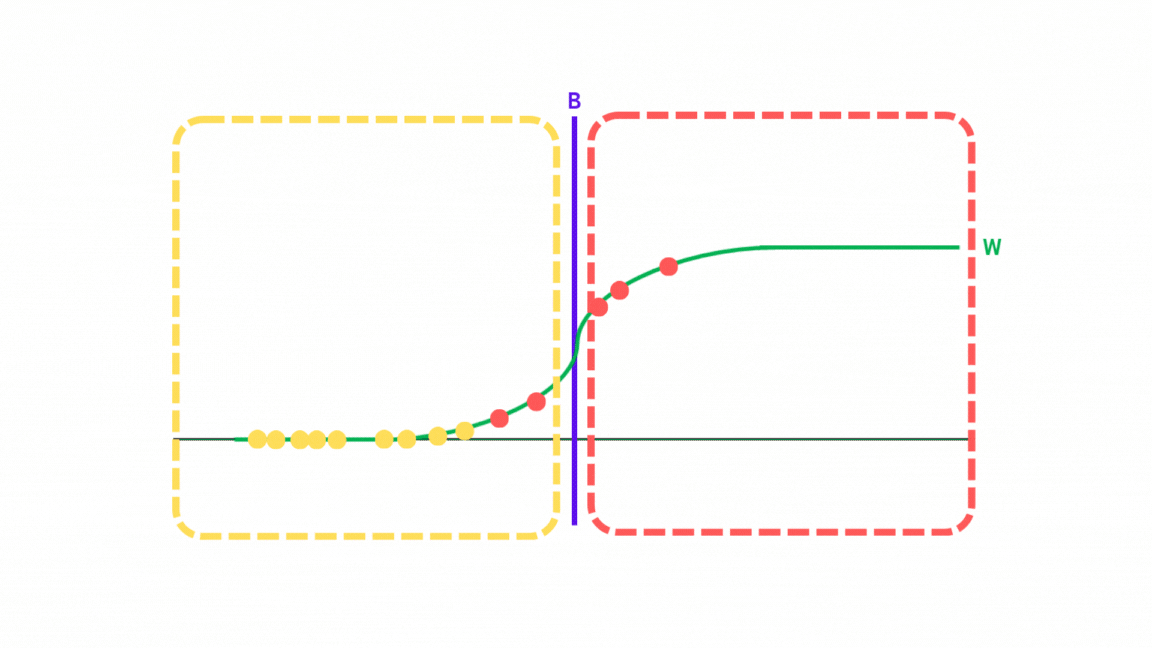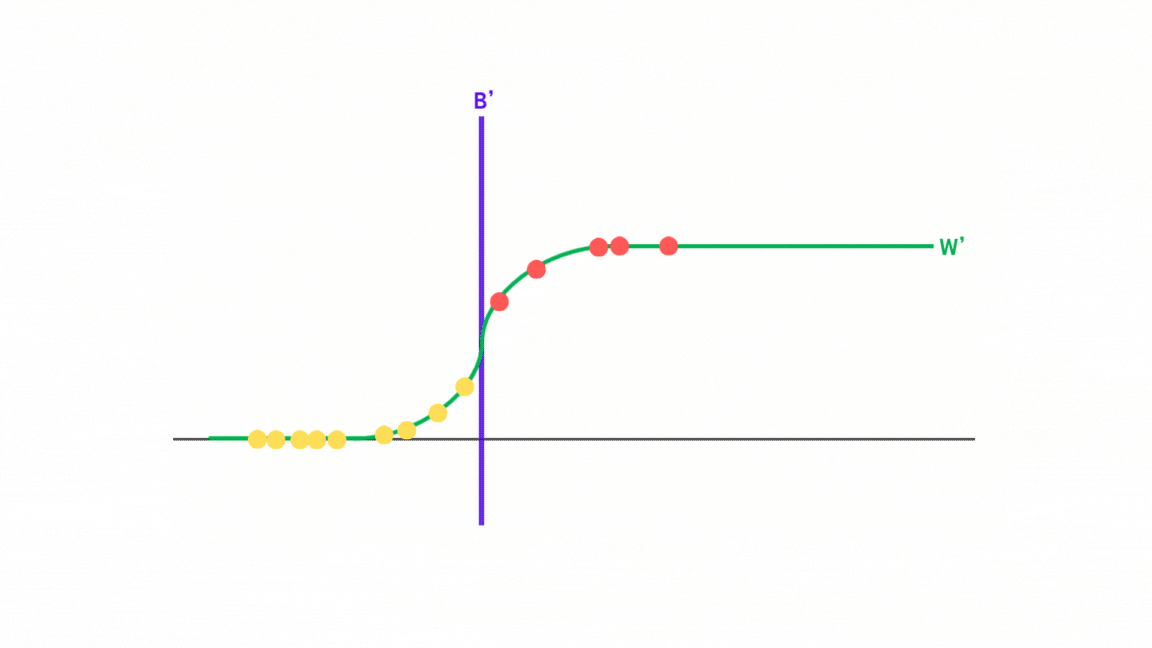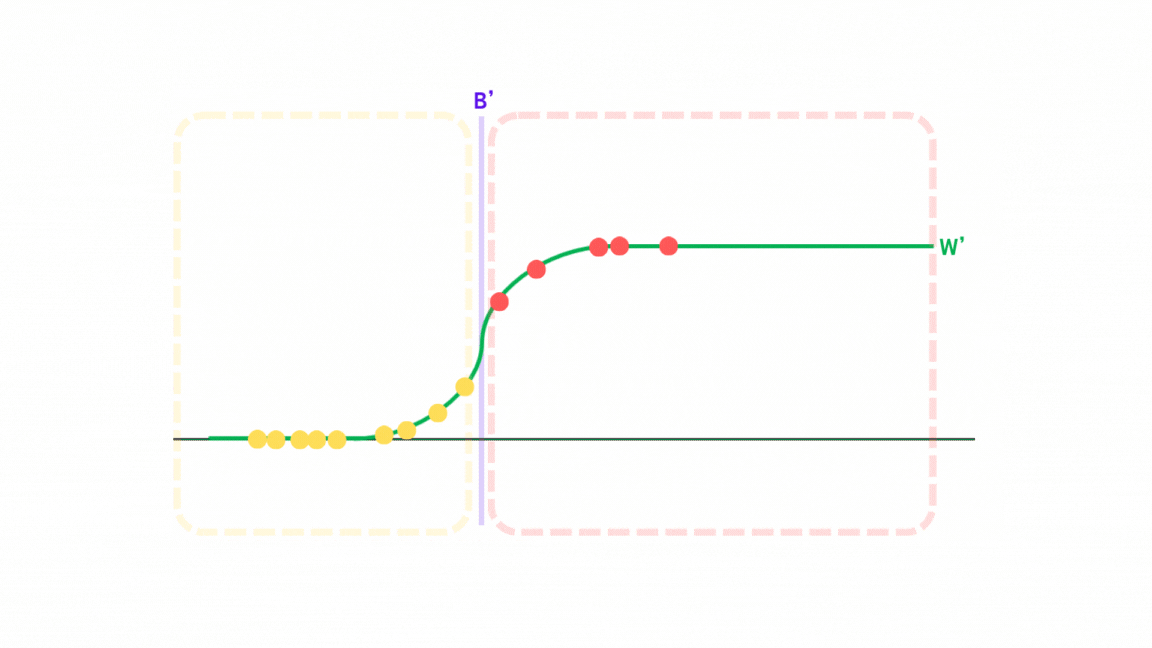
💡시그모이드 함수와 우도

시그모이드 함수

시그모이드 함수 역시 입력 값을 특정 값으로 사상시키는 함수로, 전체 실수 값을 0~1 사이의 값으로 변환해주는 함수이다.

$$Sigmoid=\frac{1}{1+exp(-z)},z=wx+b$$

$w$는 시그모이드 곡선의 기울기를, $b$는 시그모이드 값의 중앙값에 대한 x값을 결정한다.

---

우도

시그모이드 함수는 입력값에 대해 0~1 사이의 값을 변환한다. 0~1사이의 값은 곧 확률값의 형태로 볼 수 있으나, 어쨌든 변환된 모든 값의 총합이 1이 되리라 보장하지 않으므로 확률밀도함수 모델을 적용해 구할 수는 없고, 대신 이들의 곱을 통해 '그럴싸한 정도'인 우도를 구할 수 있다.

그렇다면 최적의 function은 곧 우도값을 최대로 만드는 함수일 것이다. 쉽게 생각하면, 시그모이드 함수에 로그를 취한 후 미분을 하는 방법이 있겠다. 하지만 이렇게 되면 실제 레이블값이 어찌 되었건 w벡터는 단순히 데이터세트 벡터 세트 X와의 유사성을 최소로 하는 벡터가 될 것이다.

이것이 문제가 되는 경우는 특정 레이블 그룹에서 극단적인 x가 존재하는 상황이다. 온전히 데이터값의 분포로만 W를 구하면 분류가 부정확할 것이다.

따라서, 로지스틱 회귀에서는 우도값이 최대, 즉 '그럴싸 함'이 최대가 되는 W를 구한다. 최대우도 $L(w)$를 구하는 식은 아래와 같다. 확률의 곱으로 최대 우도를 구한다.

$$L(w)=p(t^{(1)},...,t^{(N)}|x^{(1)},...,x^{(N)};w)=\prod _{i=1}^{N}p(t^{(i)}|x^{(i)};w)$$$$p(t^{(i)}|x^{(i)};w)=(1-p(C=0|x^{(i)};w){)}^{t^{(i)}}p(C=0|x^{(i)};w{)}^{1-t^{(i)}}$$$$p(C=0|x^{(i)};w)=\frac{1}{1+exp(-z)},z=wx+b$$

위 식은 학습 데이터가 iid 조건을 충족한다는 전제에서 성립한다. 이렇게 되면, 옳은 레이블이 아니나 시그모이드값이 크게 나오는 경우라도 지수값이 0이 되면서 해당 시그모이드 값이 무시되고 반대의 확률값만 곱해지게 된다.

최대의 $L(w)$를 구하기 위해선 미분을 적용하기 위해 자연로그를 취한다. 이렇게 하면 w에 대해 미분이 가능해진다. 여기서 더 나아가, 계산의 편리함을 위해 로그 값에 음수를 곱한다. 그러면 기울기가 최소가 되는 지점을 구하게 된다.

여기서 목적함수가 되는 비용함수(cost function)는 $-logL(w)$이다. 비용함수가 최소가 되는 w값이 곧 로그 우도를 최대로 하는 함수이다.

💡왜 음수로 바꾸는가

사실 로그 값에 대해 최대가 되는 w를 찾는 것도 동일한 결과를 도출한다. 다만 굳이 음수값으로 바꿔 구하는 이유는 목적함수를 비용함수로 정의했기 때문이다. 비용함수의 goal이 최소지점이므로, 이러한 관점에 맞춰 값을 구하기 위해 굳이 음수로 값을 취해 구하는 것이다. 구태여 비용함수로 정의해 구하는 이유는 최저값 계산이 더 간편하기 때문이라고 한다.

따라서, $L(w)$에 대한 최종적인 수식은 아래와 같다.

$$L(w)=\prod _{i=1}^N{(1-\frac{1}{1+e^{-z^{(i)}}})}^{t(i)}{(\frac{1}{1+e^{-z^{(i)}}})}^{1-t(i)}$$$$L(w)=\prod _{i=1}^N{(\frac{e^{-z^{(i)}}}{1+e^{-z^{(i)}}})}^{t(i)}{(\frac{1}{1+e^{-z^{(i)}}})}^{1-t(i)}$$$$=\prod _{i=1}^N{(\frac{e^{-z^{(i)}}}{1+e^{-z^{(i)}}})}^{t(i)}{(\frac{1}{1+e^{-z^{(i)}}})}^{-t(i)}{(\frac{1}{1+e^{-z^{(i)}}})}^1$$$$=\prod _{i=1}^N(e^{-z^{(i)}}{)}^{t(i)}{(\frac{1}{1+e^{-z^{(i)}}})}^1=\prod _{i=1}^N{(e^{-z^{(i)}})}^{t(i)}{(1+e^{-z^{(i)}})}^{-1}$$

로그를 씌워 최종적으로 정리하면 아래와 같다.

$$logL(w)=l(w)=-\sum _{i=1}^N(t(i)z^{(i)})-\sum _{i=1}^{N}lo{g}_e(1+e^{-z^{(i)}})$$

비용함수의 형태로 정의하면 다음과 같다. 이제부터는 이 비용함수를 $w$에 대해 미분하도록 하겠다.

$$-\ell (w)=\sum _{i=1}^N(t(i)z^{(i)})+\sum _{i=1}^{N}lo{g}_e(1+e^{-z^{(i)}})$$

이제 $w_i$에 대한 편미분을 통해 최적의 $W$ 벡터를 찾으면 된다. 그런데 여기서 문제가 있다. $w$에 대해 미분해야 하는데, 식은 치환변수인 $z$로 작성되어 있다. 따라서 여기서는 연쇄법칙에 따른 매개변수 미분을 진행한다.

이때, $x_i$의 차원수만큼 $w_i$가 존재할 것이고, $w_i$ 하나를 찾기위해선 N개의 데이터에 대해 연산해야 한다. 즉, $w_1...w_D$의 미분계수가 존재하고, 이는 미분계수 벡터의 형태로 나타낼 수 있다.

$$▽W=[\frac{\partial }{\partial w_1},\frac{\partial }{\partial w_1},...,\frac{\partial }{\partial w_D}{]}^T$$

이것을 이제 데이터 세트 하나씩 곱하여 미분하면 된다. 아마 벡터 연산으로 나타내면 아래와 같은 모양일 것이다. 모든 식에서 0이 나오도록 연립방정식을 풀면 된다.

우행렬의 열벡터 각각은 i번째의 x 벡터이다. 보통은 벡터연산으로 $z=W^T{X}_i$로 풀기에, 아래와 같이 행렬로 연산한다.

$$\left[\begin{array}{cccccc}\frac{\partial }{\partial w_1}& \frac{\partial }{\partial w_2}& & ...& & \frac{\partial }{\partial w_D}\end{array}\right]\left[\begin{array}{ccc}{t}^{(1)}{w_1{x}_1}^{(1)}+log(1+e^{-{w_1{x}_1}^{(1)}})& ...& t^{(N)}{w_1{x}_1}^{(N)}+log(1+e^{-{w_1{x}_1}^{(N)}})\\ t^{(1)}{w_2{x}_2}^{(1)}+log(1+e^{-{w_2{x}_2}^{(1)}})& ...& t^{(N)}{w_2{x}_2}^{(N)}+log(1+e^{-{w_2{x}_2}^{(N)}})\\ & ...& \\ t^{(1)}{w_D{x}_D}^{(1)}+log(1+e^{-{w_D{x}_D}^{(1)}})& ...& t^{(N)}{w_D{x}_D}^{(N)}+log(1+e^{-{w_D{x}_D}^{(N)}})\end{array}\right]$$$$=▽W^T\cdot \left[\begin{array}{ccc}{t}^{(1)}{W}^T{X}_1+log(1+e^{-W^T{X}_1})& ...& t^{(N)}{W}^T{X}_N+log(1+e^{-W^T{X}_N})\end{array}\right]$$

여기서 $\frac{\partial }{\partial w_1}[t^{(1)}{w_1{x}_1}^{(1)}+log(1+e^{-{w_1{x}_1}^{(1)}})]$의 식만 계산 해보자.

💡로그의 미분

case1 $y=lnx$

$$\frac{dy}{dx}=\frac{1}{x}$$

case2 $y=lo{g}_{a}x$

$$\frac{dy}{dx}=\frac{1}{xlna}$$

case3 $y=lnkx$

$$\frac{dy}{dx}=\frac{1}{x}$$

이제부터는 특정 스칼라 값들에 대한 연산이므로 $w_1=w,x_1^{(1)}=x$로 간단하게 표현하겠다.

자연로그가 있으므로, 자연로그 내부의 식은 $u$로 치환하여, 연쇄 법칙을 적용하여 미분해야 한다.

1. $w$에 대해 미분하기

$$\frac{\partial }{\partial w}twx+\frac{\partial }{\partial w}ln(u),u=1+e^{-wx}$$$$tx+\frac{\partial }{\partial u}ln(u)\frac{\partial u}{\partial w}$$

2. $u$에 대해 미분하기

$$\frac{\partial }{\partial u}ln(u)=\frac{1}{u}$$

3. $u$를 $w$에 대해 미분하기

$$\frac{\partial u}{\partial w}=-x{e}^{-wx}$$

4. 대입하기

$$tx+(1+e^{-wx}{)}^{-1}(-x{e}^{-wx})=x(t-(1+e^{-wx}{)}^{-1}(e^{-wx}))$$

5. 미분값이 0이 되는 지점의 w 구하기

• $t=1$ 인 경우

$$x+(1+e^{-wx}{)}^{-1}(-x{e}^{-wx})=x(1-(1+e^{-wx}{)}^{-1}(e^{-wx}))=0$$$$1-\frac{e^{-wx}}{(1+e^{-wx})}=0$$$$\frac{e^{-wx}}{(1+e^{-wx})}=1$$$$e^{-wx}=1+e^{-wx}$$$$-wx=ln(1+e^{-wx})$$$$w=-\frac{ln(1+e^{-wx})}{x}$$

---

exponential의 미분은 매우 까다롭다. 그런데, 이런 exponential에 대한 미분을 NxD회 실행해야 하므로, 하나의 CPU를 이용해 순차적으로 미분방정식을 푸는 것은 매우 비효율적이고, 사실상 불가능한 일일 것이다.

따라서, 딥러닝의 학습 시에는 그래픽 연산에 최적화된 프로세서인 GPU를 이용해, $d_n$에 대해 동시다발적으로 다수의 데이터에서 미분이 계산될 수 있도록 병렬연산을 진행한다. 즉, $t_1$의 시간에 N개의 $w_1$에 대한 미분 연산이 동시에 진행된다는 것이다. GPU 개수가 많으면 많을 수록, 동시에 계산할 수 있는 차원 수도 많아지므로 훨씬 빨라진다.

물론, 제아무리 GPU와 같은 하드웨어의 도움을 받아 연산을 효율화 할 수 있다고 하더라도, 기본적으로는 차원 수를 줄인다던가, 데이터 샘플링을 통해 대표성을 갖는 데이터세트에 대해서만 학습을 진행한다던가 하는 방법을 함께 사용한다.